90 Number Bingo Cards
On This Page
1-90 Number Bingo myfreebingocards.com Safety First! Before you print all your bingo cards, please print a test page to check they come out the right size and color. Printable Bingo Cards 90 Numbers – These Printable Number Bingo Cards will appear in useful anytime you need to get information from somebody. Whenever you want to obtain the information that you need, you can just type the person’s identify and you also will get 1 2.
Introduction
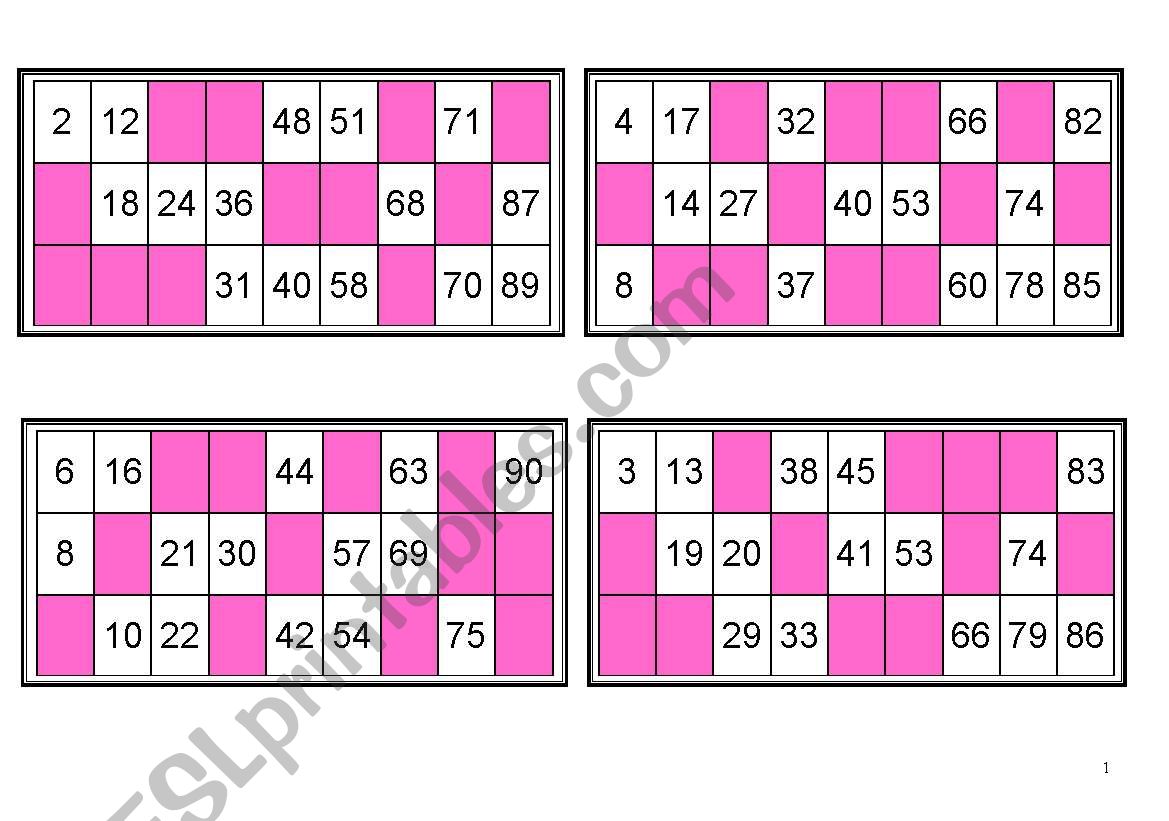
Unlike American bingo with a 5 by 5 card with numbers from 1 to 75, in Europe and South America bingo is often played with a 3 by 9 card with numbers from 1 to 90. Below is an example.
As the example shows, the card contains 3 rows and 9 columns. On each row are exactly 5 numbers. The other four cells in each row are blank, or free squares. From other examples I have seen the first row contains the numbers 1 to 10, the second 11 to 20, and so on, but mathematically this doesn't matter. Winning events I have heard of all are based on covering rows only, so mathematically speaking the game could played on a 3 by 5 card with all numbers covered, the odds would be the same.
90 Number Bingo Cards
The purpose of this appendix is to show the probability of covering (1) at least one row, (2) at least 2 rows, and (3) all three rows, in any given number of calls from 5 to 90. For example, the table shows the probability of covering at least one row in 50 calls on any one card is 0.139289864, or 13.93%.
90 Number Bingo ProbabilitiesExpand
| Calls | One Row Probability | Two Rows Probability | Three Rows Probability | One Row Inverse Probability | Two Rows Inverse Probability | Three Rows Inverse Probability |
|---|---|---|---|---|---|---|
| 5 | 0.0000000683 | 0 | 0 | 1 in 14649756 | ||
| 6 | 0.0000004096 | 0 | 0 | 1 in 2441626 | ||
| 7 | 0.0000014335 | 0 | 0 | 1 in 697607 | ||
| 8 | 0.0000038226 | 0 | 0 | 1 in 261603 | ||
| 9 | 0.0000086008 | 0 | 0 | 1 in 116268 | ||
| 10 | 0.0000172017 | 0 | 0 | 1 in 58134 | 1 in 1906881827301 | |
| 11 | 0.0000315364 | 0 | 0 | 1 in 31709 | 1 in 173352893391 | |
| 12 | 0.0000540623 | 0 | 0 | 1 in 18497 | 1 in 28892148899 | |
| 13 | 0.0000878511 | 0.0000000001 | 0 | 1 in 11383 | 1 in 6667418977 | |
| 14 | 0.000136657 | 0.0000000005 | 0 | 1 in 7318 | 1 in 1904976850 | |
| 15 | 0.0002049848 | 0.0000000016 | 0 | 1 in 4878 | 1 in 634992301 | 1 in 45795673964460800 |
| 16 | 0.0002981578 | 0.0000000042 | 0 | 1 in 3354 | 1 in 238122146 | 1 in 2862229622778800 |
| 17 | 0.0004223859 | 0.0000000102 | 0 | 1 in 2368 | 1 in 98050336 | 1 in 336732896797506 |
| 18 | 0.0005848332 | 0.0000000229 | 0 | 1 in 1710 | 1 in 43577969 | 1 in 56122149466251 |
| 19 | 0.0007936849 | 0.0000000484 | 0 | 1 in 1260 | 1 in 20642236 | 1 in 11815189361316 |
| 20 | 0.0010582143 | 0.0000000969 | 0 | 1 in 945 | 1 in 10321154 | 1 in 2953797340329 |
| 21 | 0.0013888484 | 0.000000185 | 0 | 1 in 720 | 1 in 5406350 | 1 in 843942097237 |
| 22 | 0.0017972335 | 0.0000003391 | 0 | 1 in 556 | 1 in 2948945 | 1 in 268527030939 |
| 23 | 0.0022962984 | 0.0000005999 | 0 | 1 in 435 | 1 in 1666818 | 1 in 93400706414 |
| 24 | 0.0029003168 | 0.0000010285 | 0 | 1 in 345 | 1 in 972330 | 1 in 35025264905 |
| 25 | 0.0036249674 | 0.000001714 | 0.0000000001 | 1 in 276 | 1 in 583414 | 1 in 14010105962 |
| 26 | 0.0044873918 | 0.0000027852 | 0.0000000002 | 1 in 223 | 1 in 359038 | 1 in 5927352522 |
| 27 | 0.0055062482 | 0.0000044234 | 0.0000000004 | 1 in 182 | 1 in 226072 | 1 in 2634378899 |
| 28 | 0.006701763 | 0.0000068803 | 0.0000000008 | 1 in 149 | 1 in 145342 | 1 in 1223104489 |
| 29 | 0.008095776 | 0.0000105007 | 0.0000000017 | 1 in 124 | 1 in 95232 | 1 in 590464236 |
| 30 | 0.0097117813 | 0.0000157493 | 0.0000000034 | 1 in 103 | 1 in 63495 | 1 in 295232118 |
| 31 | 0.0115749612 | 0.0000232459 | 0.0000000066 | 1 in 86 | 1 in 43018 | 1 in 152377867 |
| 32 | 0.0137122121 | 0.0000338066 | 0.0000000124 | 1 in 73 | 1 in 29580 | 1 in 80950742 |
| 33 | 0.0161521615 | 0.0000484952 | 0.0000000226 | 1 in 62 | 1 in 20621 | 1 in 44154950 |
| 34 | 0.0189251748 | 0.0000686847 | 0.0000000405 | 1 in 53 | 1 in 14559 | 1 in 24674825 |
| 35 | 0.0220633488 | 0.0000961302 | 0.0000000709 | 1 in 45 | 1 in 10403 | 1 in 14099900 |
| 36 | 0.0256004928 | 0.0001330566 | 0.0000001216 | 1 in 39 | 1 in 7516 | 1 in 8224942 |
| 37 | 0.0295720915 | 0.0001822611 | 0.0000002045 | 1 in 34 | 1 in 5487 | 1 in 4890506 |
| 38 | 0.0340152517 | 0.0002472336 | 0.0000003378 | 1 in 29 | 1 in 4045 | 1 in 2960043 |
| 39 | 0.0389686274 | 0.0003322973 | 0.000000549 | 1 in 26 | 1 in 3009 | 1 in 1821565 |
| 40 | 0.0444723213 | 0.0004427703 | 0.0000008784 | 1 in 22 | 1 in 2259 | 1 in 1138478 |
| 41 | 0.0505677613 | 0.0005851526 | 0.0000013851 | 1 in 20 | 1 in 1709 | 1 in 721962 |
| 42 | 0.0572975481 | 0.0007673395 | 0.0000021546 | 1 in 17 | 1 in 1303 | 1 in 464118 |
| 43 | 0.0647052697 | 0.0009988639 | 0.0000033089 | 1 in 15 | 1 in 1001 | 1 in 302217 |
| 44 | 0.0728352824 | 0.0012911709 | 0.0000050204 | 1 in 14 | 1 in 774 | 1 in 199188 |
| 45 | 0.081732452 | 0.0016579252 | 0.0000075306 | 1 in 12 | 1 in 603 | 1 in 132792 |
| 46 | 0.0914418539 | 0.002115356 | 0.0000111744 | 1 in 11 | 1 in 473 | 1 in 89490 |
| 47 | 0.1020084273 | 0.0026826381 | 0.0000164124 | 1 in 10 | 1 in 373 | 1 in 60930 |
| 48 | 0.1134765801 | 0.0033823132 | 0.0000238726 | 1 in 8.8 | 1 in 296 | 1 in 41889 |
| 49 | 0.1258897424 | 0.0042407513 | 0.0000344046 | 1 in 7.9 | 1 in 236 | 1 in 29066 |
| 50 | 0.1392898636 | 0.0052886518 | 0.0000491494 | 1 in 7.2 | 1 in 189 | 1 in 20346 |
| 51 | 0.1537168505 | 0.0065615844 | 0.0000696283 | 1 in 6.5 | 1 in 152 | 1 in 14362 |
| 52 | 0.1692079444 | 0.0081005673 | 0.000097856 | 1 in 5.9 | 1 in 123 | 1 in 10219 |
| 53 | 0.1857970345 | 0.0099526798 | 0.0001364834 | 1 in 5.4 | 1 in 100 | 1 in 7327 |
| 54 | 0.203513905 | 0.0121717032 | 0.000188977 | 1 in 4.9 | 1 in 82 | 1 in 5292 |
| 55 | 0.2223834172 | 0.0148187832 | 0.0002598433 | 1 in 4.5 | 1 in 67 | 1 in 3848 |
| 56 | 0.2424246244 | 0.0179631039 | 0.000354908 | 1 in 4.1 | 1 in 56 | 1 in 2818 |
| 57 | 0.2636498229 | 0.0216825599 | 0.0004816608 | 1 in 3.8 | 1 in 46 | 1 in 2076 |
| 58 | 0.2860635412 | 0.0260644094 | 0.000649682 | 1 in 3.5 | 1 in 38 | 1 in 1539 |
| 59 | 0.309661472 | 0.031205888 | 0.0008711645 | 1 in 3.2 | 1 in 32 | 1 in 1148 |
| 60 | 0.3344293554 | 0.037214755 | 0.0011615527 | 1 in 3 | 1 in 27 | 1 in 861 |
| 61 | 0.3603418208 | 0.0442097423 | 0.0015403199 | 1 in 2.8 | 1 in 23 | 1 in 649 |
| 62 | 0.387361203 | 0.0523208636 | 0.0020319114 | 1 in 2.6 | 1 in 19 | 1 in 492 |
| 63 | 0.4154363465 | 0.0616895391 | 0.0026668837 | 1 in 2.4 | 1 in 16 | 1 in 375 |
| 64 | 0.4445014202 | 0.0724684766 | 0.0034832766 | 1 in 2.2 | 1 in 14 | 1 in 287 |
| 65 | 0.4744747683 | 0.0848212433 | 0.0045282596 | 1 in 2.1 | 1 in 12 | 1 in 221 |
| 66 | 0.5052578274 | 0.0989214474 | 0.0058601006 | 1 in 2 | 1 in 10 | 1 in 171 |
| 67 | 0.5367341493 | 0.1149514356 | 0.0075505143 | 1 in 1.86 | 1 in 8.7 | 1 in 132 |
| 68 | 0.568768574 | 0.1331003983 | 0.0096874523 | 1 in 1.76 | 1 in 7.5 | 1 in 103 |
| 69 | 0.6012066069 | 0.153561752 | 0.0123784113 | 1 in 1.66 | 1 in 6.5 | 1 in 81 |
| 70 | 0.6338740649 | 0.1765296538 | 0.0157543416 | 1 in 1.58 | 1 in 5.7 | 1 in 63 |
| 71 | 0.6665770642 | 0.2021944733 | 0.0199742546 | 1 in 1.5 | 1 in 4.9 | 1 in 50 |
| 72 | 0.6991024401 | 0.2307370275 | 0.0252306373 | 1 in 1.43 | 1 in 4.3 | 1 in 40 |
| 73 | 0.7312186968 | 0.262321349 | 0.0317558022 | 1 in 1.37 | 1 in 3.8 | 1 in 31 |
| 74 | 0.7626776074 | 0.2970857299 | 0.0398293112 | 1 in 1.31 | 1 in 3.4 | 1 in 25 |
| 75 | 0.7932165977 | 0.3351317439 | 0.049786639 | 1 in 1.26 | 1 in 3 | 1 in 20 |
| 76 | 0.8225620687 | 0.3765109088 | 0.0620292551 | 1 in 1.22 | 1 in 2.7 | 1 in 16 |
| 77 | 0.8504338369 | 0.4212086067 | 0.077036333 | 1 in 1.18 | 1 in 2.4 | 1 in 13 |
| 78 | 0.8765508925 | 0.4691248258 | 0.095378317 | 1 in 1.14 | 1 in 2.1 | 1 in 10 |
| 79 | 0.9006387073 | 0.5200512338 | 0.1177326101 | 1 in 1.11 | 1 in 1.92 | 1 in 8.5 |
| 80 | 0.9224383526 | 0.5736440281 | 0.1449016739 | 1 in 1.08 | 1 in 1.74 | 1 in 6.9 |
| 81 | 0.941717722 | 0.6293919373 | 0.1778338726 | 1 in 1.06 | 1 in 1.59 | 1 in 5.6 |
| 82 | 0.9582851926 | 0.686578675 | 0.2176474261 | 1 in 1.04 | 1 in 1.46 | 1 in 4.6 |
| 83 | 0.9720060987 | 0.7442390568 | 0.2656578878 | 1 in 1.03 | 1 in 1.34 | 1 in 3.8 |
| 84 | 0.9828224403 | 0.801107902 | 0.3234096025 | 1 in 1.02 | 1 in 1.25 | 1 in 3.1 |
| 85 | 0.9907762969 | 0.8555607343 | 0.3927116602 | 1 in 1.01 | 1 in 1.17 | 1 in 2.5 |
| 86 | 0.9960374767 | 0.9055451845 | 0.4756789123 | 1 in 1.004 | 1 in 1.1 | 1 in 2.1 |
| 87 | 0.9989359891 | 0.9485018727 | 0.5747786857 | 1 in 1.001 | 1 in 1.05 | 1 in 1.74 |
| 88 | 1 | 0.9812734082 | 0.6928838951 | 1 in 1 | 1 in 1.02 | 1 in 1.44 |
| 89 | 1 | 1 | 0.8333333333 | 1 in 1 | 1 in 1 | 1 in 1.2 |
| 90 | 1 | 1 | 1 | 1 in 1 | 1 in 1 | 1 in 1 |
Methodology: The probability of covering m marks in c calls is combin(15,m)*combin(75,c-m)/combin(90,m). Using that, you can find the probability of covering a card as combin(75,90-m)/combin(90,m). To get the probability of covering 1 or 2 rows I determined the probability that m marks would cover 1 or 2 rows. The chart below shows those probabilities, which is based on basic probability.
Printable Bingo Numbers 1 90
Rows Covered by Number of Marks
| Marks | 0 Rows | 1 Row | 2 Rows | 3 Rows | Total |
|---|---|---|---|---|---|
| 5 | 0.999001 | 0.000999 | 0 | 0 | 1 |
| 6 | 0.994006 | 0.005994 | 0 | 0 | 1 |
| 7 | 0.979021 | 0.020979 | 0 | 0 | 1 |
| 8 | 0.944056 | 0.055944 | 0 | 0 | 1 |
| 9 | 0.874126 | 0.125874 | 0 | 0 | 1 |
| 10 | 0.749251 | 0.24975 | 0.000999 | 0 | 1 |
| 11 | 0.549451 | 0.43956 | 0.010989 | 0 | 1 |
| 12 | 0.274725 | 0.659341 | 0.065934 | 0 | 1 |
| 13 | 0 | 0.714286 | 0.285714 | 0 | 1 |
| 14 | 0 | 0 | 1 | 0 | 1 |
| 15 | 0 | 0 | 0 | 1 | 1 |